Research
- Research at VU Amsterdam (2022-present)
- Post-doctoral research at CIMNE (2016-2022)
- Post-doctoral research at TUM (2013-2015)
- Early-stage research at UPC (2009-2013)
- References
Research at VU Amsterdam (2022-present)
I have recently started as Assistant Professor at the Department of Computer Science at VU Amsterdam. I will populate this section soon. For the moment, see my research at my previous position at CIMNE (2016-2022).
Post-doctoral research at CIMNE (2016-2022)
Objectives
This part of my research career starts in January 2016 and it extends up to the present. I joined CIMNE as a post-doc researcher in 2016 and I was promoted to Assistant Research Professor in view of my academic results in 2019. In CIMNE, I am pursuing a research agenda, whose main objectives are:
Developing novel parallel finite element (FE) techniques for the simulation of complex problems in science an engineering using modern supercomputers
Helping application experts to adopt these novel computational techniques to solve real-world problems
Implementing these computer tools in open-source software projects in order to foster their adoption by the scientific community
Research lines
In order to address these global objectives, my main research lines are:
RL1: Simplify mesh generation in large-scale parallel computations via embedded FE methods
RL2: Software design of scientific applications and open-source codes (the Gridap.jl project)
RL1: Simplify mesh generation in large-scale parallel computations via embedded FE methods
Mesh generation is known to be one of the main bottlenecks in real-world industrial FE simulations. Conventional FE methods require so-called body-fitted meshes, i.e., grids that conform to the geometrical boundaries of the computational domain (see Figure 1). Constructing such grids is not obvious for complex geometries. It often requires skilled humans, and it is time consuming as mesh generation is estimated to be 80% of total simulation time in industrial applications [cottrell_2009]. The goal of so-called embedded FE methods [burman_2015] (also known as unfitted or immersed methods) is to change this situation by allowing one to work on background Cartesian meshes that do not necessarily conform to the geometrical boundaries (see Figure 1). Generating such unfitted Cartesian grids is much simpler and more efficient that constructing body fitted meshes, specially in large parallel computations. One can use highly scalable octree-based mesh generators like the p4est package, which has shown excellent scaling properties up to thousands of hundreds of CPU cores.
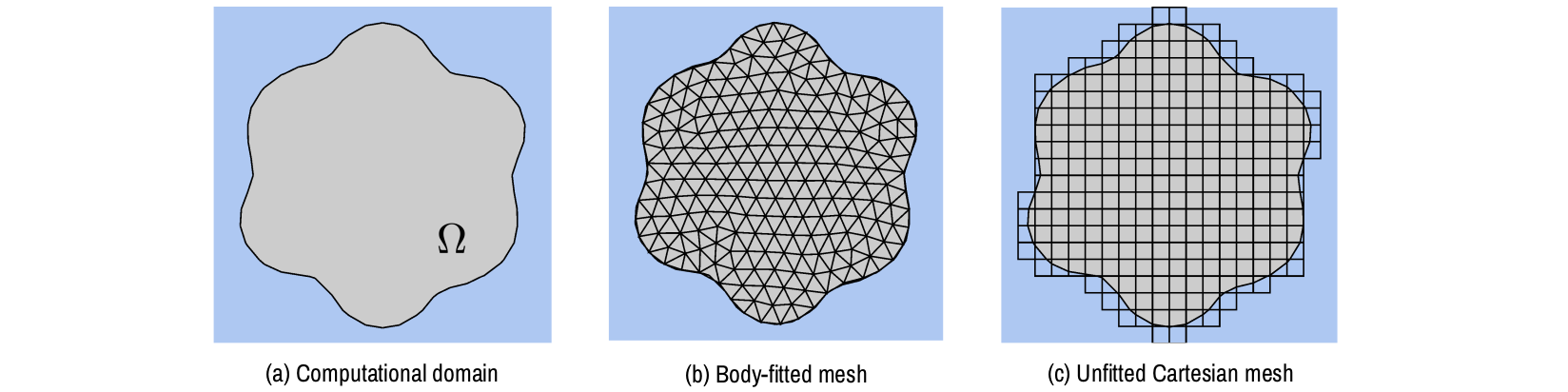
Figure 1: Body-fitted vs. unfitted meshes
However, embedded methods have known drawbacks. One of the most notorious, still an open question today, is the so-called small cut cell problem. Some cells of the unfitted mesh can be intersected by a very small part of the domain, which can lead to arbitrarily large condition numbers in the underlying discrete FE operators. This is a major issue, when dealing with large-scale simulations that require Krylov sub-space iterative linear solvers because they are very sensitive to the conditioning and spectral properties of the underlying operators. The result is that embedded methods are mainly used in small to medium problems, which can be handled with direct linear solvers (i.e., Gaussian elimination) instead of iterative procedures. One of my main research goals at CIMNE is to address the conditioning problems of embedded methods in order to allow their usage in large-scale real-world computations.
Funding
This research line has several funding sources. On the one hand, I was awarded with a Beatriu Pinós fellowship (a competitive post-doc grant issued by the Catalan autonomous government) to develop embedded FE methods for the simulation of additive manufacturing processes. With the help of this grand I was able to develop new numerical techniques and mentor a PhD student in order to adopt these new tools in his additive manufacturing simulations. This work is also framed in the H2020 project "EMUSIC", which also focuses in the same application. This research line on embedded methods has also been supported by the H2020 project "ExaQUte". In particular, I am contributor in the work package "WP1 Embedded methods", where I have lead the research associated with task "Task 1.6: Development of robust (and scalable) linear solvers for the embedded case". Another funding source is the Spanish project "SOFAST". I am involved in the works packages "WP1 Embedded methods" and "WP2 Adaptive mesh refinement". In the frame of these projects, I am currently supervising a PhD student at UPC, who is developing novel techniques to couple CAD models and embedded simulations.
Results
This research line has lead to several major research results, which are detailed as follows.
Multi-level domain decomposition for embedded finite element methods
In FE analysis, the current way to solve linear systems at large-scales is using iterative Krylov sub-space methods in combination with parallel and scalable preconditioners. Unfortunately, existing preconditioners like algebraic multigrid (AMG) [briggs_2000] or multi-level domain decomposition [toselli_2005] are mainly designed for body-fitted meshes and cannot readily deal with the ill-conditioning associated with small cut cells.
Specific precontinoners for unfitted methods have been proposed in the literature in different contexts, but they are mainly serial non-scalable algorithms. This has motivated me to develop novel techniques in order to enable the usage of embedded method in much larger computations. As a first approach, I have considered BDDC preconditioners to solve such problems at large scales. This choice is motivated by the fact that BDDC methods are among the most scalable preconditioners for FE analysis. In particular, the BDDC methods implemented in my research team have shown an excellent weak scaling up to 458,752 cores and 30 billion unknowns [badia_2016]. Unfortunately, conventional BDDC preconditioners loose they optimal qualities, when the underlying problem is discretized with an unfitted grid. Thus, available BDDC solvers cannot be considered in combination with embedded FE methods.
In order to revert this unfavorable situation, I have introduced a novel BDDC method specifically tailored to deal with embedded grids. The proposed method is based on a modification of the coarse space of the BDDC solver, which makes it robust with respect to badly cut cells. The method has been shown to be algorithmically weak scalable for a wide range of 3D complex geometries. That is, the number of iterations needed to reach convergence in the preconditioned linear solver is asymptotically independent of the problem size (see Figure 2). This work is published in [badia_2017]) and has been presented in several conferences both at national and international level.
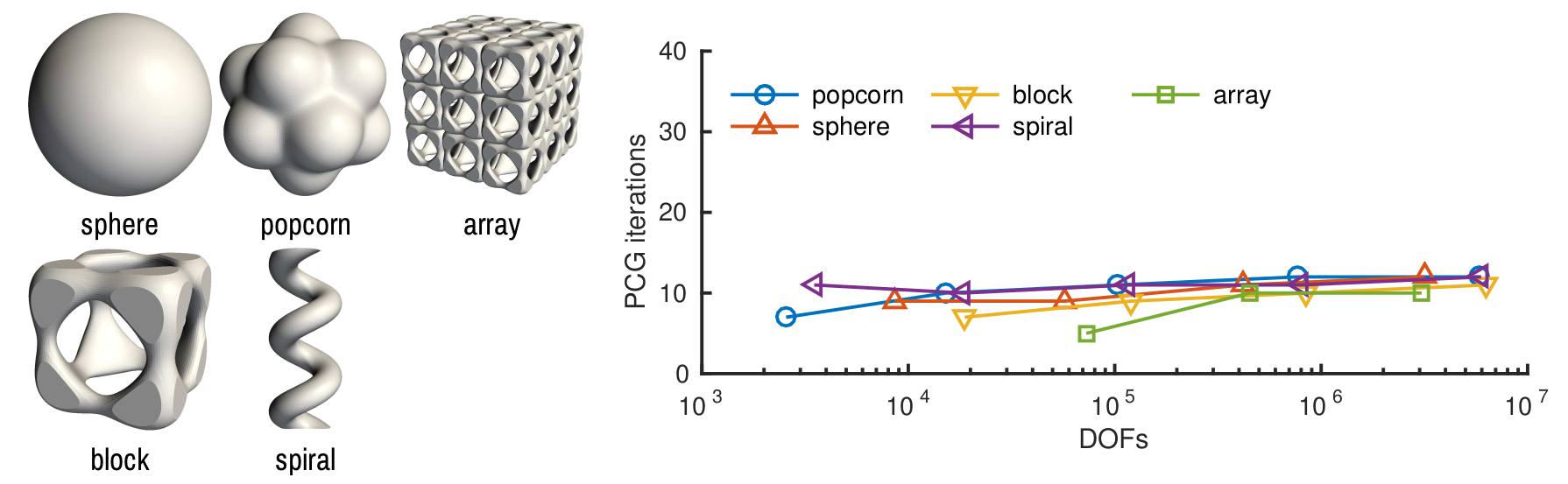
Figure 2: BDDC for embedded methods in a weak scaling test for a Poisson problem on different complex 3D geometries. A perfect weak scaling of the linear solver iterations is obtained.
The aggregated unfitted finite element method (AgFEM)
Most of the works enabling the usage of iterative linear solver in combination with embedded FE methods consider tailored preconditioners in order to deal with matrices affected by the small cut cell problem (e.g., the BDDC method for embedded grids previously presented). The main drawback of this approach is that one relies on highly customized solvers, and therefore, it is not possible to take advantage of well known and established linear solvers for FE analysis available in renowned scientific computing packages as Trilinos or PETSc. In order to address this issue, I have considered a second approach. I have developed an enhanced FE formulation that leads to linear systems, whose condition number is not affected by small cuts (see Figure 3). Therefore, they can be solved with standard linear solvers such as the AMG methods available in Trilinos or PETSc.
The enhanced FE formulation is called the aggregated unfitted finite element method (AgFEM), which is based on removal of shape functions associated with badly cut cells by introducing carefully designed constraints. The formulation of AgFEM shares the good properties of body-fitted FE methods such as stability, condition number bounds, optimal convergence, and continuity with respect to data. In contrast to previous works like CutFEM [burman_2015], it is easy to implement and to use in different problem types since it does not require to compute high order derivatives of the shape functions, and it does not introduce extra dissipation terms in the weak form. AgFEM has already been successfully applied to the solution of fluid [badia_2018b] and heat transfer problems [badia_2018a].
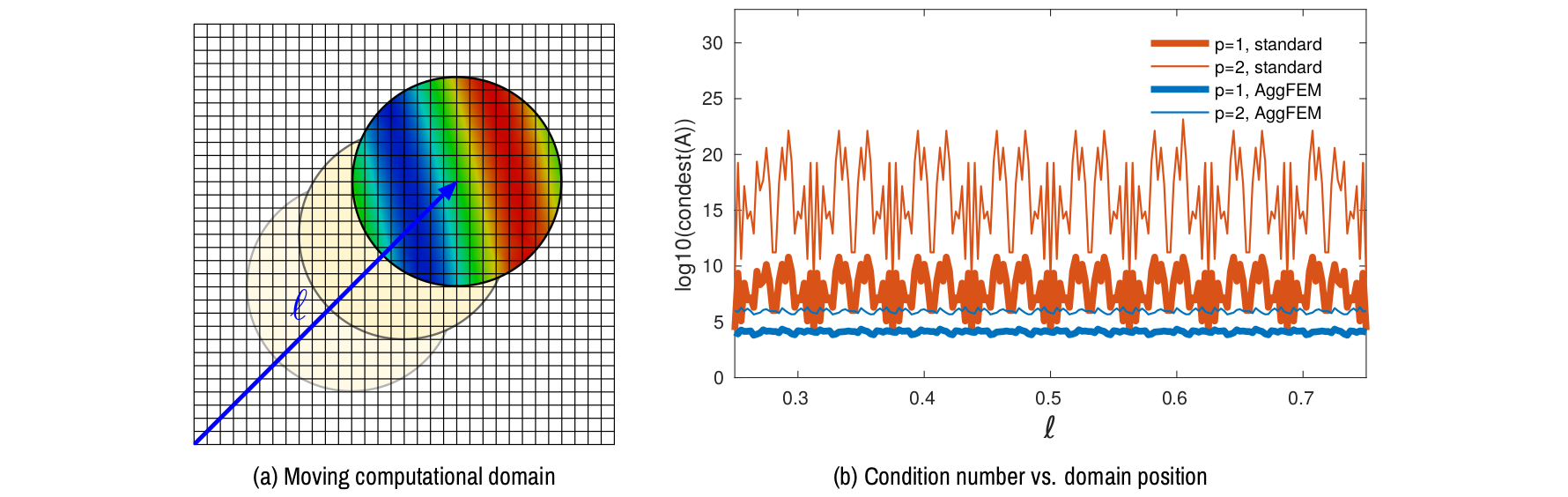
Figure 3: Poisson problem defined on a moving domain. Note that the standard embedded formulation leads to very high condition numbers, which are very sensitive to the relative position between the computational domain and the background mesh, specially for second order interpolations (). In contrast, the condition number is much lower for the enhanced formulation (the AgFEM method) and it is nearly independent of the position of the domain.
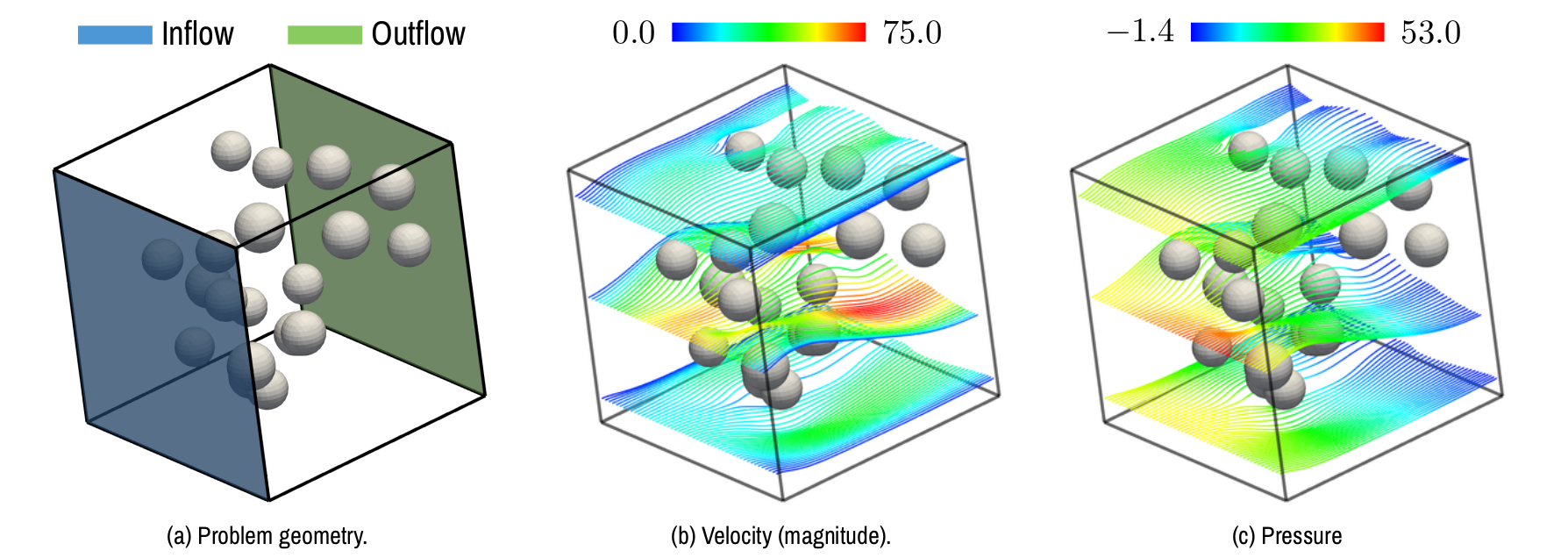
Figure 4: Numerical solution of a (dimensionless) Stokes problem using the AgFEM method (streamlines colored by velocity magnitude and pressure). This computation is carried out without constructing an unstructured body-fitted mesh thanks to the application of the AgFEM method.
Extension of AgFEM to large-scale parallel computations.
I have implemented a distributed-memory version of AgFEM in the FEMPAR software project making use of MPI for inter-processor communications. The obtained results confirmed my expectations. When using AgFEM, the resulting systems of linear algebraic equations can be effectively solved using standard AMG preconditioners. In this case, I have considered the AMG methods available in the GAMG module of the PETSc library. With the parallel AgFEM, I was able to run weak scaling tests up to 300M degrees of freedom (DOFs) and 16K processors in the Marenostrum-IV platform. The results show that the optimal behavior of AMG solvers for body-fitted meshes is also recovered for AgFEM, i.e. number of linear solver iterations asymptotically independent of problem size. To my best knowledge, this is the first time that embedded methods are successfully applied to such large scales. These results have been published in [verdugo_2019].
Extension of AgFEM to adaptive computations.
Parallel implementations and scalable solvers are essential to dramatically reduce the computation times of challenging simulations, but not sufficient in many contexts. Several problems of interest are multi-scale in nature and, thus, require different mesh resolution in different spatial locations. In this context, trying to capture the finest scales with uniform meshes in overkill and the usage of adaptive mesh refinement becomes mandatory.
Parallel mesh adaptation is a challenging operation since mesh partition and load balance needs to be carefully realized to achieve performance. In large parallel computations, Cartesian grids locally adapted with forest-of-trees (also known as octree meshes) are among the few ways to locally adapt in a scalable way. They leverage so-called space-filing curves to reduce the mesh partition and load balance to a 1d problem that can be solved very efficiently. However, the main drawback of this approach is that the resulting computational grid contains so-called hanging nodes, which require extra work when defining conforming FE interpolations. If certain conditions are not satisfied, the constraints introduced by hanging nodes may expand beyond a single layer of ghost cells, thus leading to an incorrect parallel FE solver. Unfortunately, the current literature fails to explain under which conditions this happens for generic conforming FE discretizations (i.e., not only limited to Lagrangian elements). To address this situation, I have studied the correctness of a number of algorithms and parallel data structures needed to build conforming FE discretizations on octree meshes partitioned via space-filling curves. The proposed algorithms and data structures have been implemented within the FEMPAR scientific software library, using p4est as the forest-of-trees back-end. A strong scaling study reveals remarkable scalability up to 32.2K CPU cores and 482.2M DOFs (see reference [badia_2019a] ).
In a second step, I have combined the parallel AgFEM implementation previously developed with this adaptive FE framework. The result is a novel scalable distributed-memory version of AgFEM on locally-adapted Cartesian meshes. The main novelty of the method is a two-step algorithm that carefully mixes AgFEM constraints, which get rid of the small cut cell problem, and standard hanging node constraints, which ensure trace continuity. This method requires minimum parallelization effort since it can leverage standard functionality available in existing large-scale FE codes. Numerical experiments demonstrate its optimal mesh adaptation capability, robustness to cut location and parallel efficiency, on classical Poisson hp-adaptivity benchmarks. This work opens the path to functional and geometrical error-driven dynamic mesh adaptation with the AgFEM method in large-scale realistic scenarios. A research paper detailing this work is published in [badia_2021]).
Embedded finite element methods for 3D printing simulations
One the main driving applications of my research on embedded FE methods has been the simulation of additive manufacturing processes using advanced large-scale FEs. This is the main topic of my Beatriu Pinós fellowship and the EU H2020 project "EMUSIC", were I have participated as researcher. Additive manufacturing (also known as 3D printing) is an advanced manufacturing method used to build physical objects directly from 3D computer designs by the superposition of thin layers of materials such as metals, polymers or composites. 3D printers have been described in numerous occasions as a revolutionary technology with the potential to radically transform the manufacturing industry. However, high-energy sources used to melt metal powders during the printing process induce thermo-mechanical shape distortions and residual stresses, that deteriorate the geometrical quality and the requested material properties. Currently, the standard industrial practice to optimize the printing process in order to obtain quality components is through experimental testing, which is expensive and time consuming since it requires the production of hundreds of prototypes before reaching the final piece. Fortunately, predictive computer simulations can potentially be used to validate the process parameters before printing the component. However, current simulation software still has important limitations when it comes to predict shape distortions and residual stresses in complex settings with an acceptable level of accuracy and an acceptable time frame.

Figure 5: Snapshots of a thermal 3D printing simulation using the AgFEM method in order to effectively represent the geometry of the growing piece.
I have contributed to develop novel computational tools able to provide much faster and accurate results. In particular, generating computational meshes for additive manufacturing simulations is particularly challenging and time consuming. The shape of the 3D printed object grows in time, layer-by-layer, as it is produced. Capturing the growing shape requires a different mesh for each time step to represent the portion of the piece that has been produced so far. It is obvious that generating thousands of independent meshes with conventional methods is virtually impossible. Thus, embedded methods are well suited in this context. I have applied the AgFEM method to additive manufacturing simulations in collaboration with a PhD student of my research team (see Figure 5).
Current and future work
I plan to continue working on my current research line on large-scale FE solvers and embedded methods and its application to challenging engineering problems. I will extend these techniques to more challenging problem types and collaborate with application experts in order to simulate relevant real-world cases.
RL2: Software design of scientific applications and open-source projects
I have recently started a new research line whose goal is to develop a new generation of open-source FE codes since the development of high-performance scientific software for the numerical approximation of PDEs is a key research area with a broad impact in advanced scientific and engineering applications. Existing partial differential equation (PDE) solvers like FE codes are usually written in compiled programming languages introduced several decades ago, mainly C/C++ and Fortran 95/03/08. These languages are considered for performance reasons, but they are also related to poor code productivity. In contrast, interpreted languages like Python or MATLAB allow one to write scripts and applications in much less lines of code, boosting code productivity, but they lead to much slower programs. A trade-off between performance and productivity is usually achieved in scientific software libraries like FEniCS by combining an efficient C/C++ computational back-end with a user-friendly high-level Python user front-end. However, this approach is not satisfactory, when researchers need to extend these libraries with new features since they are forced to learn and modify a complex C/C++ back-end instead of benefiting from the productivity expected from the Python front-end. This problem is referred to as the two-language problem.
Fortunately, recent advances in compiler technology are starting to revert this situation. In the field of scientific computing, Julia is a new computer language that combines the performance of compiled languages with the productivity of interpreted ones by using recent advances in compiler technology like type inference and just-in-time compilation. As a result, the same language can be used both for the back-end and the front-end, thus eliminating the two-language problem. Based on this novel paradigm, I have started the Gridap.jl project [badia_2020], a new generation, open-source, FE framework completely written in the Julia programming language. Gridap.jl allows users to write FE applications in a notation almost one-to-one to the mathematical notation used to define the PDE weak form. For instance, see, in Figure 6, how a Poisson equation on a complex 3D domain can be solved in Gridap.jl with few lines of code. To my best knowledge, only libraries like FEniCS are able to achieve such compact user interfaces, but they are based on sophisticated compilers of variational forms, which generate, compile and link a specialized C++ back-end for the problem at hand. One of the limitations of this approach is that form compilers are rigid systems, not designed to be extended by average users. In contrast, Gridap.jl is based on a much simpler approach. It leverages the Julia just-in-time compiler to generate efficient problem-specific code without the need to maintain a custom compiler of variational forms.

Figure 6: User code to solve a 3D Poisson equation in Gridap.jl and view of the corresponding numerical solution. Note that the bilinear and linear forms of the problem, a and l, are specified with a syntax closely related to their mathematical notation thanks to an advanced software design based on the Julia computer language.
Funding
Gridap.jl appears as one of the two PDE codes selected to implement new novel FE methods in a "Discovery Project" of the Australian Research Council (ref: DP210103092, $475000) co-lead by my collaborator at Monash University Prof. Santiago Badia. In the framework of this project, new collaborators are expected to joint and contribute in the expansion of the project. In addition, Gridap.jl has been accepted as a NumFOCUS affiliated project. The mission of NumFOCUS is to promote open practices in research, data, and scientific computing by serving as a fiscal sponsor for open source projects and organizing community-driven educational programs. Being an affiliated project, Gridap.jl is eligible to participate in NumFOCUS funding schemes and other events like the participation in the Google Summer of Code under the NumFOCUS umbrella. In 2021, we participated with the projects "Visualizing PDE approximations in Julia with Gridap.jl and Makie.jl" and "A fast finite element interpolator in Gridap.jl".
Results
Initial release of the open-source finite element project Gridap.jl
The first immediate result in this research line is the initial release of the project, whose source code is freely available at github under a MIT software license. In addition, a related article has been published in the "Journal of Open Scientific Software" (see reference [badia_2020]). Gridap.jl is already a fully functional general-purpose FE library ready to solve linear, non-linear, steady-state, and time-dependent PDEs. It already provides different types of conforming FE methods like nodal Lagrangian elements for grad-conforming approximations (e.g., for linear elasticity or thermal analysis) or non-nodal interpolations like Raviart-Thomas for div-conforming approximations (e.g., for flow in porous media). Discontinuous Galerkin schemes are also supported. Gridap.jl is currently used by several research groups worldwide in institutions such as Monash University, MIT, TU Delft, UPC, and CIMNE. A set of introductory tutorials to the library is available and a Gitter chat to ask questions and interact with the Gridap.jl community.
GridapEmbedded.jl: a Gridap.jl plugging providing embedded finite element methods
The Gridap.jl project is designed to be an extensible package ecosystem with several plugins that extend the functionality of the core repository. In particular, GridapEmbedded.jl is an extension that implements embedded FE methods. At this moment, it provides embedded methods based on classical ghost-penalty or methods based on AgFEM, being the only known open source package to provide both types of methods. GridapEmmbedded.jl will be the basis to implement the new space-time methods since it is implemented in a dimension-implemented fashion allowing to consider 4D meshes in the future.
Current and future work
GridapDistributed.jl: a Gridap.jl plugging for parallel distributed computations.
At this moment, Gridap.jl provides mainly serial algorithms and needs to be extended to parallel computations in order to cope with large-scale realistic simulations. To this end, I have started the plugin GridapDistributed.jl, whose goal is to provide the parallel functionality needed in parallel distributed-memory computations. I am designing a set of extensible distributed data structures that allow one to implement parallel algorithms in a generic way independent on the parallel computing environment (e.g., MPI or the Julia build-in distributed mode) used to run the computations. This is specially handy for developing new code since it allows one to debug parallel algorithms by running an emulated distributed computation in a standard (sequential) Julia session and using standard serial debuggers. Once the code works with the emulated parallel mode, it can be automatically deployed in a supercomputer via an MPI back-end implemented for this purpose. Thus, the package provides a very convenient way of developing parallel algorithms, while achieving the performance of MPI-based applications. This will help to develop new parallel FE methods in a very effective way. In particular, PhD students not necessarily experts in the MPI library can benefit from this framework to develop their parallel algorithms. At this moment, I have been able to solve the Poisson equation with up to 1B cells on 16K processors with GridapDistributed.jl on Gadi (an Australian super-computer) and I expect to further mature and extend the capabilities of this library.
Leveraging the Gridap.jl ecosystem to solve problems in science and engineering.
Several researchers have already realized the potential benefits of using the Gridap.jl framework for their applications and have asked to me for collaboration. My plan is to keep growing a network of scientific collaborators that use the library in several contexts, in order to increase my changes of publishing more research papers and to find relevant topics for preparing project proposals.
Post-doctoral research at TUM (2013-2015)
In this post-doc stay, I have developed parallel AMG solvers for the solution of large systems of linear algebraic equations associated with the FE discretization of complex multi-physics problems. The main goal of this research was to provide a general framework able to be applied to several problem types. In particular, this work was applied to fluid-structure interaction (FSI), thermo-mechanical coupling, and human respiratory mechanics among others.
General framework for the solution of coupled problems with monolithic schemes
The numerical simulation of coupled problems via discretization techniques such as the FE method requires special solution strategies for solving the coupling between the underlying physical fields. The so-called partitioned methods [felippa_2001] are often the preferred choice in industrial applications because they allow to reuse existing (black-box) solvers for the individual fields. However, this approach is unstable for many challenging strongly coupled problems [forster_2007] and, therefore, another family of methods called monolithic are required in a variety of complex settings. It has also been shown that monolithic schemes are often preferable in terms of efficiency as compared to partitioned ones. For that reason, this approach has been the preferred option for solving many strongly coupled problems in the literature. However, the price to be paid for the extra robustness of monolithic methods is a more challenging system of linear equations. The system matrix is a big sparse matrix with a special block structure representing each of the underlying physical fields and frequently has a very bad condition number. In real-world applications, iterative methods such as GMRES are used to attack this linear system, which requires efficient preconditioners for addressing the bad conditioning of the problem. Selecting a suitable preconditioner is the key point in the solution process.
The standard approach to design preconditioners for coupled problems is to use approximated block inverses in order to untangle the coupling between the physical fields, and then, to use efficient AMG solvers for the resulting uncoupled problems. The drawback of these methods is that the coupling is resolved only at the finest grid level. Thus, using efficient AMG solvers for the underlying problems does not necessarily imply a good treatment of the coupling and a fast global solution. This drawback is overcome by Gee et al. [gee_2011], who propose an enhanced block preconditioner (referred to as monolithic AMG) for FSI applications, which enforces the coupling at all grid levels, and often results in a better solver performance. Monolithic AMG preconditioners are a promising approach for other coupled problems as well but, this strategy was only applied to FSI. In order to allow the usage of this enhanced AMG methods for a wide range of problem types, I have developed an general computational framework based on monolithic AMG techniques. For comparison purposes, conventional AMG solvers were also included. The method was implemented in the high performance multi-physics code BACI and it was published in a Q1 journal (see reference [verdugo_2016a]). This framework has been used at TUM since then, and it has been considered by several papers in top international journals (see, e.g., [kremheller_2018][fang_2018]), with a wide range of applications including simulation of vascular tumor growth and simulations of lithium ion cells.
Solvers for the thermo-mechanical coupling in rocket nozzles
In the framework of the German research project "Fundamental Technologies for the Development of Future Space-Transport-System Components under High Thermal and Mechanical Loads", I have applied the general linear solver framework to the simulation of the thermo-mechanical coupling in rocket nozzles. I exemplary show here the performance of the developed preconditioners. The nozzle geometry (see Figures 7 and 8) and other problem parameters are inspired by the "Vulcain" rocket engine installed in the Ariane space launcher, see [verdugo_2016a] for further details.
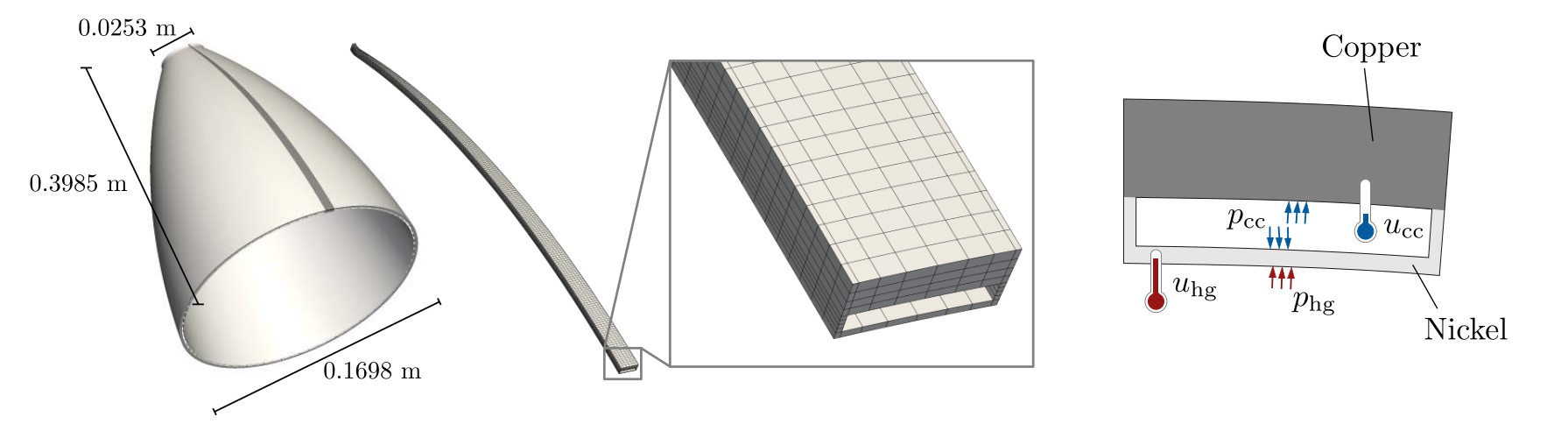
Figure 7: Rocket nozzle example: Full geometry of the nozzle (left), computational domain including one cooling channel (center), and generic cross section of the computational domain with the applied thermo-mechanical loads (right)
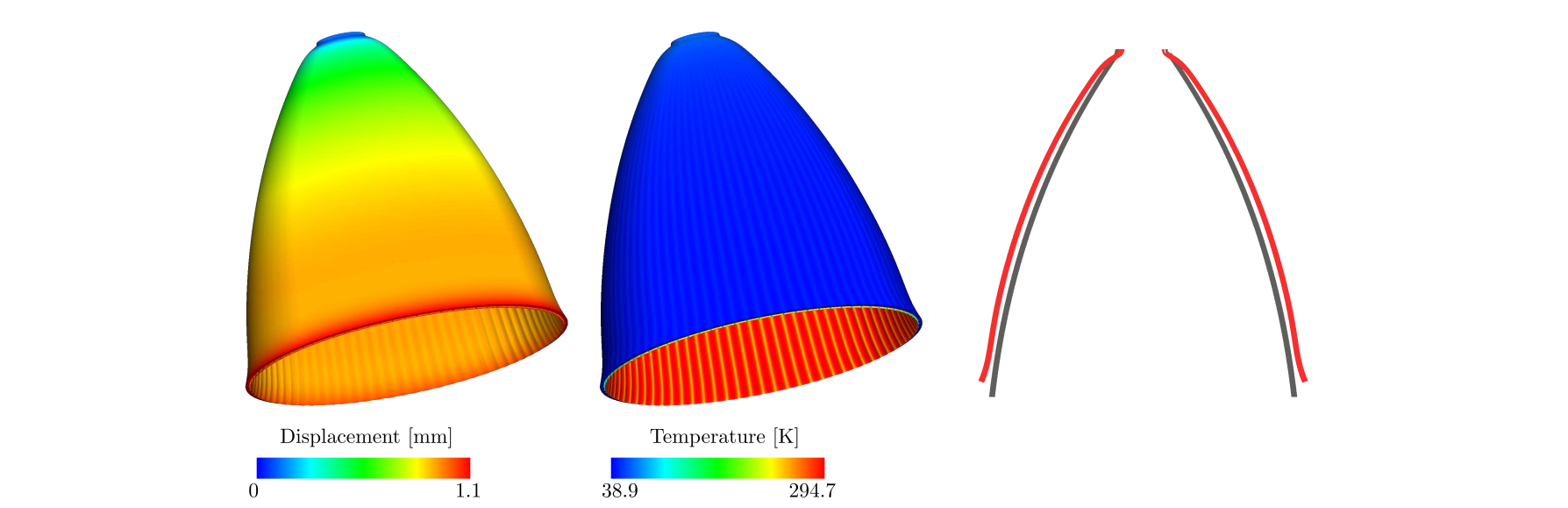
Figure 8: Rocket nozzle example: Deformation of the nozzle (left), temperature distribution (center) and original and deformed longitudinal section (right). The results are given at time s and the deformation is magnified 20 times.
After the usual space and time discretization, the simulation results into a non-linear problem to be solved at each time step, which is handled with a monolithic Newton scheme. At each Newton iteration, the associated monolithic linear system of equations is solved with a GMRES method preconditioned with four different solvers available in our computational framework. The first method, namely BGS(AMG), considers an outer block Gauss-Seidel (BGS) scheme for uncoupling the fields and then independent AMG solvers are used to handle the thermal and mechanical problems separately. The second method, namely SIMPLE(AMG), is a similar method that considers an idea based on the SIMPLE method [elman_2008] for uncoupling the fields instead of BGS. The third method, namely AMG(BGS), is an extension of the monolithic AMG solver to a generic coupled problem. Finally, the fourth method, namely BGS(DD), is an outer BGS for uncoupling the fields and then standard single-level additive Schwartz preconditioners are used to attack the uncoupled problems. The fourth method is one of the most simple parallel preconditioners that can be considered in such a problem, and therefore, it is considered here as a reference. All this solvers could be built easily by means of parameter lists using the general preconditioning framework.
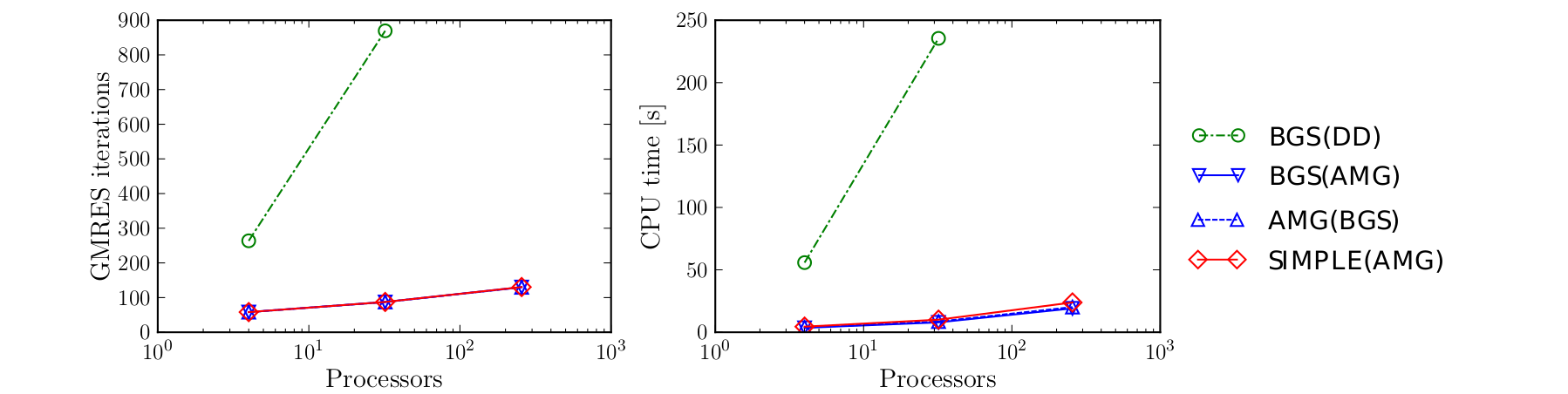
Figure 9: Rocket nozzle example: Results of the weak scalability study. The CPU times include the setup costs of the preconditioner.
The performance of the preconditioners is studied with a weak scalability test, see Figure 9. In this experiment, the ratio between processors and DOFs is kept constant with a value about 12500 DOF/processor. The multi-grid methods AMG(BGS), BGS(AMG) and SIMPLE(AMG) have a very good scalability as the iteration count and CPU time of the linear solver increase only mildly with the problem size. On the other hand, the single-level method BGS(DD) is not scalable since the solver time strongly grows as the problem size increases. The performance of the single-level method BGS(DD) is particularly poor in this complex example which demonstrates that multi-grid preconditioners such as AMG(BGS), BGS(AMG) and SIMPLE(AMG) are required in this challenging setting. In conclusion, the AMG solvers implemented in our generic computational framework were able to solve this complex example efficiently.
Efficient solvers for respiratory mechanics
Another application of the general linear solver framework has been the simulation of human respiratory mechanics. In recent years, advances have been made towards more protective ventilation strategies [tobin_2001] trying to minimize negative side effects of the treatment, but it is still not fully clear what is the best ventilation strategy for a specific patient. Advanced modeling and simulation offer the possibility of predicting the mechanical response of the respiratory system under different ventilation scenarios, and give an opportunity to design better patient-tailored treatments. However, simulating the human lung poses several computational challenges including large and multiply coupled systems of linear equations. Thus, the underlying motivation of this work is to enable the efficient simulation of virtual lung models on high-performance computing platforms in order to assess mechanical ventilation strategies and contributing to design more protective patient-specific ventilation treatments.
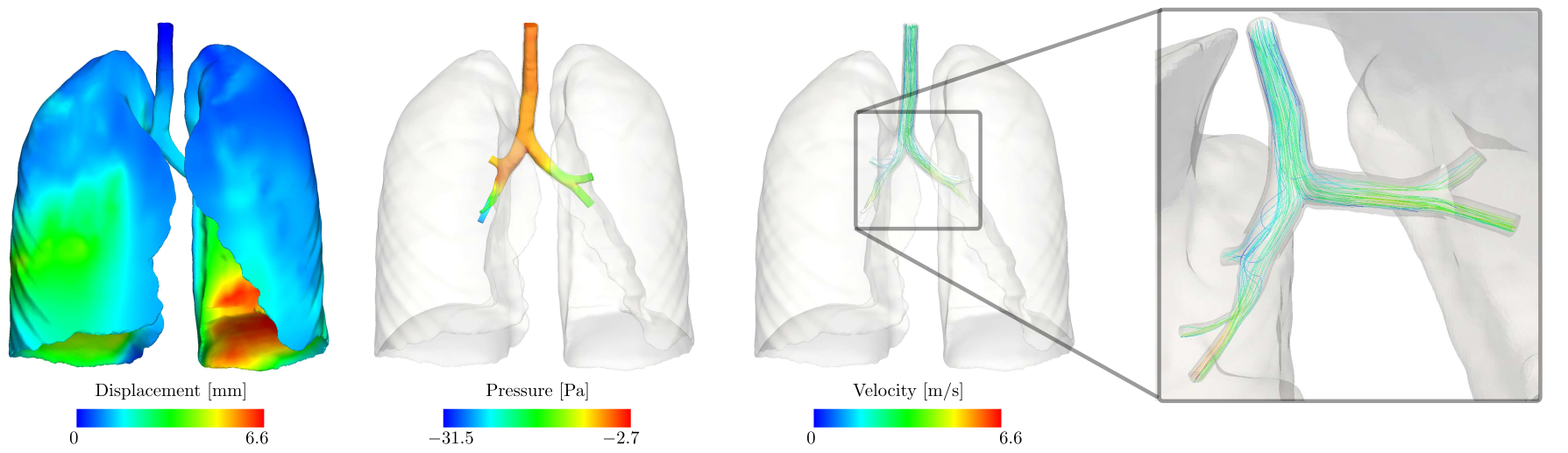
Figure 10: Patient-specific lung example: Numerical solution of the lung model consisting of the structural displacement (left), fluid pressure (center) and fluid velocity (right) at time s.
The system of linear equations to be solved in this application is essentially the monolithic system arising in FSI extended by additional algebraic constraints. The introduction of these constraints leads to a saddle point problem that cannot be solved with usual FSI preconditioners available in the literature. The key ingredient in this work is to use the idea of the semi-implicit method for pressure-linked equations (SIMPLE) for getting rid of the saddle point structure, resulting in a standard FSI problem that can be treated with available techniques. Even though the lung model is a complex multi-physics problem (see Figure 10), the numerical examples show that the resulting preconditioners approaches the optimal performance (see Figure 11). Moreover, the preconditioners are robust enough to deal with physiologically relevant simulations involving complex real-world patient-specific lung geometries. The same approach is applicable to other challenging biomedical applications where coupling between flow and tissue deformation is modeled with additional algebraic constraints. This work has lead to 1 paper in a Q1 journal (see reference [verdugo_2016b]). In the framework of this research, I have been junior co-PI in the Bavarian regional project "Efficient solvers for coupled problems in respiratory mechanics".
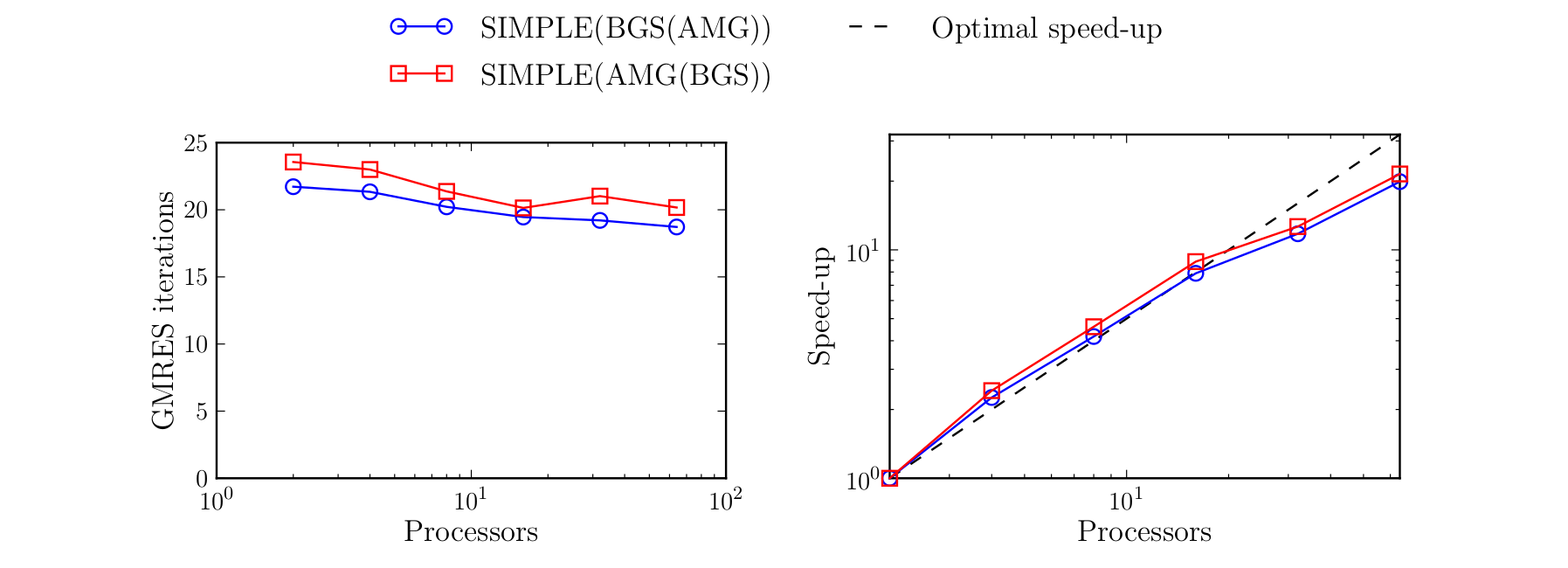
Figure 11: Patient-specific lung example: Results of the strong scalability test. The figure shows the dependence of the linear solver iterations with respect to the number of processors (left), and the parallel speed up (right).
Early-stage research at UPC (2009-2013)
PhD thesis overview
My PhD thesis, entitled "Error assessment and adaptivity for structural transient dynamics", is devoted to the development of new automatic adaptive mesh refinement tools and goal-oriented error assessment techniques in the context of structural dynamics. Any FE based simulation has an intrinsic amount of error with respect to the exact solution of the selected physical model. Being aware of this error is of notorious importance if sensitive engineering decisions are taken on the basis of the numerical results. Assessing the error in elliptic problems (as structural statics) was a well known problem at the time of this PhD thesis. However, assessing the error in other more challenging problem types such as structural transient dynamics was an open research topic. In this context, most of the works provided a posteriori error estimates of the energy norm of the discretization error. The challenge was to develop so-called goal-oriented error estimates for this application. That is, a posteriori approximations of the error in a given quantity of interest of the underlying physical problem. This goal-oriented error estimation is specially well suited for real-world industrial applications since it provides information of the quality of the computed solution in the targeted quantities instead of a global function norm.
The main contributions of the PhD thesis are 1) the introduction of a novel technique to compute bounds of the (unknown) discretization error in a given quantity of interest (see reference [verdugo_2012]), 2) a goal-oriented space-time adaptive mesh refinement method specifically designed for efficiency in transient problems (see references [casadei_2013][verdugo_2014a]), and 3) a novel paradigm for error estimation in transient problems based on a new type of quantities of interest (see reference [verdugo_2013]). I published a review paper with my main thesis results (see reference [verdugo_2014b]) in the "Archives of Computational Methods in Engineering", which is the 1st ranked journal in the category "mathematics, interdisciplinary applications" of the Journal Citation Reports (JCR) in the year of publication. In the following, I briefly introduce items 2) and 3), which are the major thesis novelties.
Modal-based goal-oriented error assessment and adaptive mesh refinement
Goal-oriented error estimation and adaptivity is particularly challenging in time-dependent problems. Assessing the error in the quantity of interest requires introducing an auxiliary problem, referred to as the adjoint or dual problem [becker_2001]. The main difficulty is associated with the fact that the adjoint solution has to be solved backwards in time. This means that, in order to assess the error by weighting the residual of the direct (or forward) solution with the adjoint (or backward) solution, at least one of the two solutions have to be stored in the full time-space domain. In non-linear problems, the situation is even worse because the full forward problem has to be computed and stored to define the backwards adjoint. This means that assessing the error of each iteration of the forward problem potentially requires computing a different backward adjoint. The conventional approach to alleviate the storage requirements is to use checkpointing, where the forward solution is stored only at a small number of pre-selected time points. These stored snapshots are used as initial conditions on each sub-interval for recomputing the forward solution during the backwards adjoint computation. This approach mitigates the storage requirements, but for some applications, recomputing the forward solution repeatedly can be still too expensive.
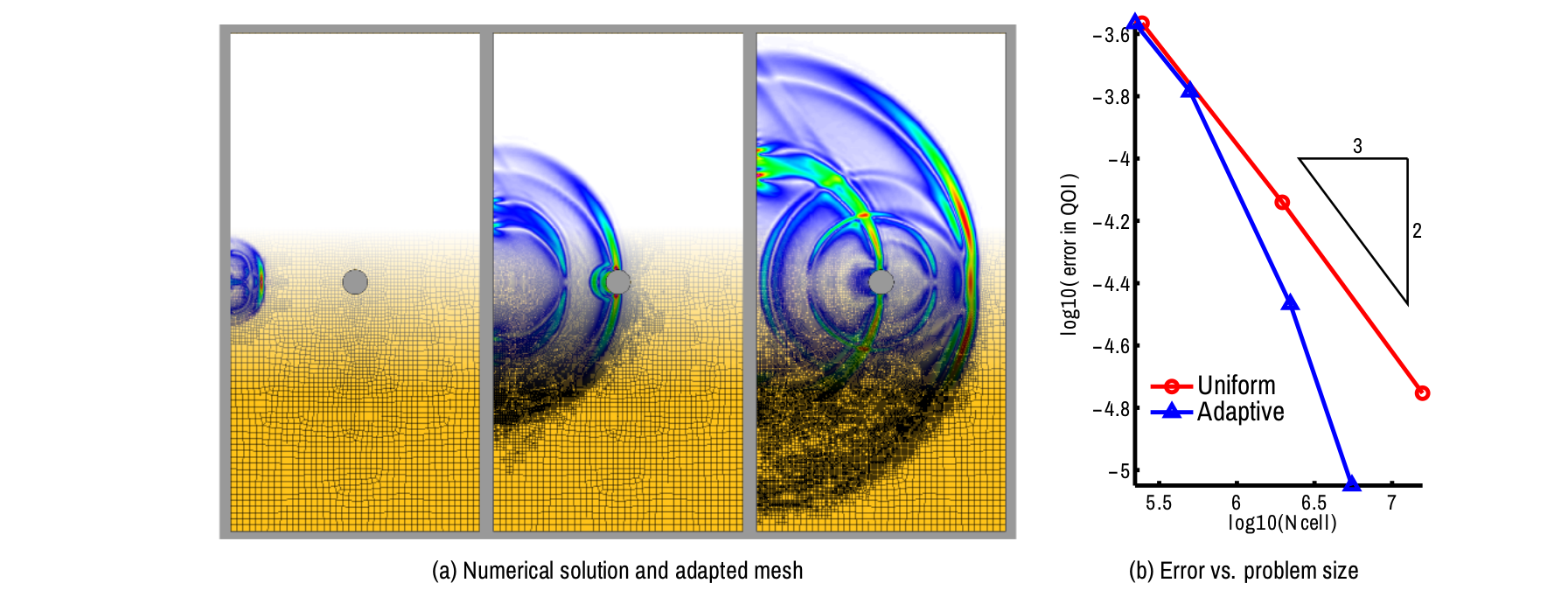
Figure 12: Simulation of elastic waves propagating in a perforated plate. The underlying space-time discretization has been automatically adapted using the goal-oriented error estimators in [verdugo_2013]. A smaller number of mesh elements are required with the adapted meshes than with uniform discretizations in order to achieve the same level of accuracy.
In the thesis, I have proposed an alternative approach based on a well known technique for structural dynamics: modal analysis. The modal-based strategy is particularly well suited for computing the adjoint problem associated with some particular quantities of interest. Following this approach, the adjoint solution is computed and stored for each vibration mode instead of for each time step, which reduces the storage requirements enormously. Using this novel approach, one can compute efficiently local error indicators that for each element and time step in the chosen discretization. This information can be used to automatically increase the resolution of the space and time discretizations only in the regions, where it is actually needed, leading to efficient computations (see Figure 12).
A novel a-posteriori error estimation paradigm based on time-dependent quantities of interest
Virtually all the literature on goal-oriented a posteriori error assessment is based on scalar quantities of interest. While this approach is well suited for steady-state problems, a single scalar value does not give enough pieces of information about a complex space-time solution. For this reason, the preferred quantities of interest in time-dependent problems are typically the history (or evolution) of the space average of the solution in a sub-region of the domain, which are referred to as time-line dependent quantities of interest [verdugo_2013]. At the time of this PhD thesis, there was no error estimation method for this kind of quantities in the literature. One of the main thesis contributions is a new paradigm for a posteriori error estimation using this new type of quantities of interest.
As already announced, in conventional goal-oriented error assessment in a given scalar quality, one needs to introduce and solve an adjoint problem. Dealing with time-line dependent quantities is much more challenging. A time-line dependent quantity can be understood as a family of infinite scalar quantities (one for each time point in the selected computation time interval). Thus, one needs the solution of a family of infinite adjoint problems. This is computationally un-affordable in practice. However, for a number of meaningful cases, I have mathematically proven in reference [verdugo_2013] that all this adjoint problems are the equivalent after a translation of the time variable. This fundamental result is the crucial observation that allows one to assess the error in the time-line dependent quantities with an affordable cost. In addition, using a modal-based approximation of the adjoint problem allows one to accurately estimate the error in this new type of quantities in an efficient way (see Figure 13).
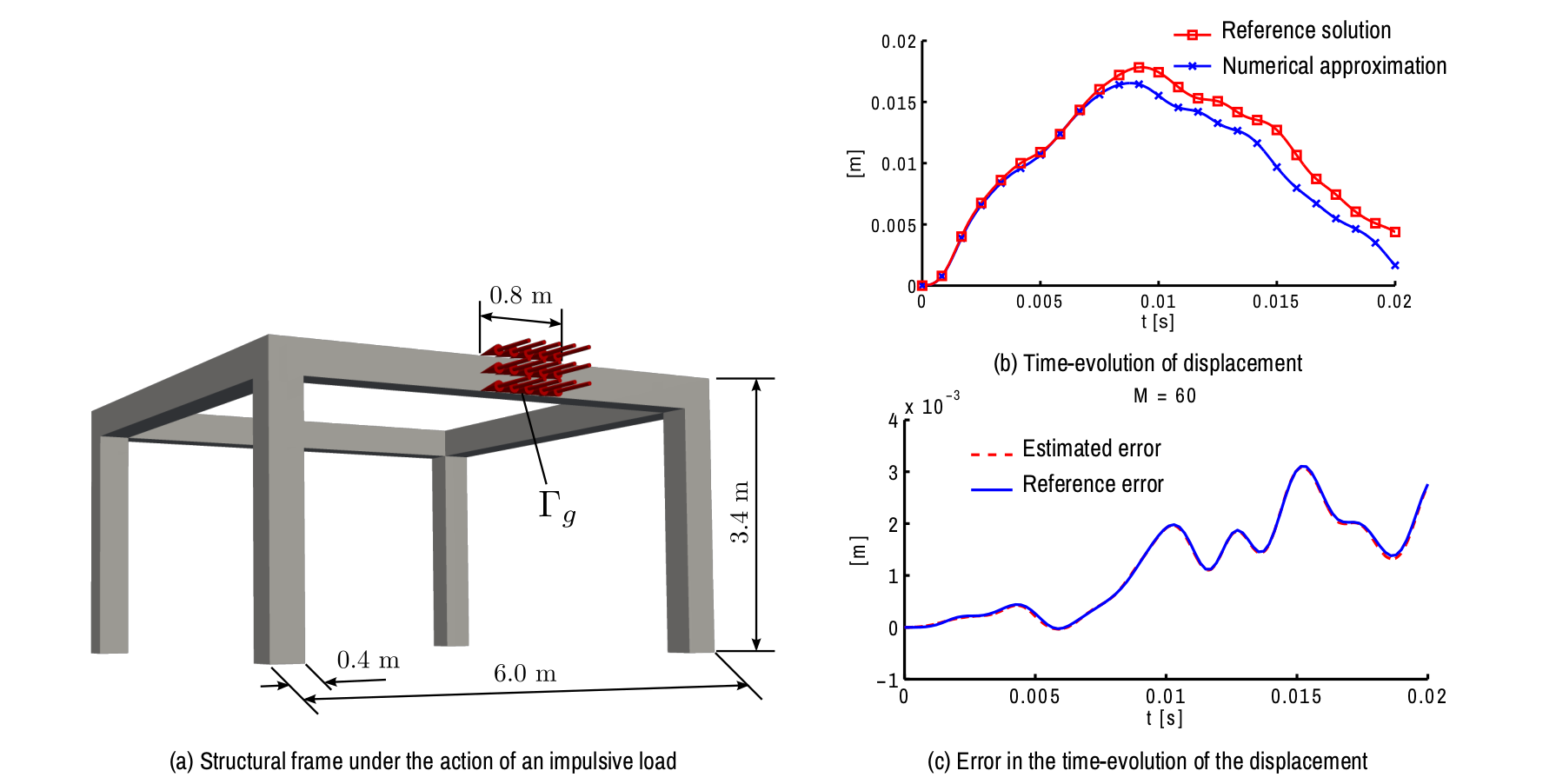
Figure 13: Error estimation of a time-line dependent quantity of interest (in this case the time-evolution of the averaged displacement at region ). Note that by approximating the family of adjoint problems associated with this quantity using only 60 vibration modes, an accurate estimation of the numerical error is achieved.
References
[badia_2016] S. Badia, A.F. Martín, and J. Principe. Multilevel Balancing Domain Decomposition at Extreme Scales. SIAM Journal on Scientific Computing, 38(1): C22–C52, 2016. DOI: 10.1137/15M1013511.
[badia_2017] S. Badia and F. Verdugo. Robust and scalable domain decomposition solvers for unfitted finite element methods. Journal of Computational and Applied Mathematics, 344: 740–759, 2018. DOI: 10.1016/j.cam.2017.09.034.
[badia_2018a] S. Badia, F. Verdugo, and A.F. Martín. The aggregated unfitted finite element method for elliptic problems. Computer Methods in Applied Mechanics and Engineering, 336: 533–553, 2018. DOI: 10.1016/j.cma.2018.03.022.
[badia_2018b] S. Badia, A.F. Martín, and F. Verdugo. Mixed Aggregated Finite Element Methods for the Unfitted Discretization of the Stokes Problem. SIAM Journal on Scientific Computing, 40(6): B1541–B1576, 2018. DOI: 10.1137/18M1185624.
[badia_2019a] S. Badia, A.F. Martín, E. Neiva, and F. Verdugo. A generic finite element framework on parallel tree-based adaptive meshes. SIAM Journal on Scientific Computing, 42(6): C436–C468, 2020. DOI: 10.1137/20M1328786.
[badia_2020] S. Badia and F. Verdugo. Gridap: An extensible Finite Element toolbox in Julia. Journal of Open Source Software, 5(52), 2020. DOI: 10.21105/joss.02520.
[badia_2021] S. Badia, A.F. Martín, E. Neiva, and F. Verdugo. The aggregated unfitted finite element method on parallel tree-based adaptive meshes. SIAM Journal on Scientific Computing, 43: C203–C234, 2021. DOI: 10.1137/20M1344512.
[becker_2001] R. Becker and R. Rannacher. An optimal control approach to a posteriori error estimation in finite element methods. Acta Numerica, 10: 1–102, 2001. DOI: 10.1017/S0962492901000010.
[briggs_2000] W.L. Briggs, V.E. Henson, and S.F. McCormick. A Multigrid Tutorial, Second Edition. Society for Industrial and Applied Mathematics, 2000. DOI: 10.1137/1.9780898719505.
[burman_2015] E. Burman, S. Claus, P. Hansbo, M.G. Larson, and A. Massing. CutFEM: Discretizing Geometry and Partial Differential Equations. International Journal for Numerical Methods in Engineering, 104(7): 472–501, 2015. DOI: 10.1002/nme.4823.
[casadei_2013] F. Casadei, P. Díez, and F. Verdugo. An algorithm for mesh refinement and un-refinement in fast transient dynamics. International Journal of Computational Methods, 10(04): 1350018, 2013. DOI: 10.1142/S0219876213500187.
[cottrell_2009] J.A. Cottrell, T.J.R. Hughes, and Y.Bazilevs. Isogeometric analysis: toward integration of CAD and FEA. Wiley, 2009. DOI: 10.1002/9780470749081.ch7.
[elman_2008] H. Elman, V.E. Howle, J. Shadid, R. Shuttleworth, and R. Tuminaro. A taxonomy and comparison of parallel block multi-level preconditioners for the incompressible Navier-Stokes equations. Journal of Computational Physics, 227(3): 1790–1808, 2008. DOI: 10.1016/j.jcp.2007.09.026.
[fang_2018] R. Fang, P. Farah, A. Popp, and W.A. Wall. A monolithic, mortar-based interface coupling and solution scheme for finite element simulations of lithium-ion cells. International Journal for Numerical Methods in Engineering, 114(13): 1411–1437, 2018. DOI: 10.1002/nme.5792.
[felippa_2001] C.A. Felippa, K.C. Park, and C. Farhat. Partitioned analysis of coupled mechanical systems. Computer Methods in Applied Mechanics and Engineering, 190(24-25): 3247–3270, 2001. DOI: 10.1016/S0045-7825(00)00391-1.
[forster_2007] C. Förster, W.A. Wall, and E. Ramm. Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Computer Methods in Applied Mechanics and Engineering, 196(7): 1278–1293, 2007. DOI: 10.1016/j.cma.2006.09.002.
[gee_2011] M.W. Gee, U. Küttler, and W.A. Wall. Truly monolithic algebraic multigrid for fluid-structure interaction. International Journal for Numerical Methods in Engineering, 85(8): 987–1016, 2011. DOI: 10.1002/nme.3001.
[kremheller_2018] J. Kremheller, A.T. Vuong, L. Yoshihara, W.A. Wall, and B.A. Schrefler. A monolithic multiphase porous medium framework for (a-)vascular tumor growth. Computer Methods in Applied Mechanics and Engineering, 340: 657–683, 2018. DOI: 10.1016/j.cma.2018.06.009.
[tobin_2001] T. Martin. Advances in mechanical ventilation. The New England Journal of Medicine, 344(26): 1986–1996, 2001. DOI: 10.1056/NEJM200106283442606.
[toselli_2005] A. Toselli and O. B. Widlund. Domain Decomposition Methods — Algorithms and Theory, volume 34 of Springer Series in Computational Mathematics. Springer Berlin Heidelberg, Berlin, Heidelberg, 2005. DOI: 10.1007/b137868.
[verdugo_2012] F.~Verdugo and P. Díez. Computable bounds of functional outputs in linear visco-elastodynamics. Computer Methods in Applied Mechanics and Engineering, 245–246: 313–330, 2012. DOI: 10.1016/j.cma.2012.06.016.
[verdugo_2013] F. Verdugo, N. Parés, and P. Díez. Modal-based goal-oriented error assessment for timeline-dependent quantities in transient dynamics. Int. J. Numer. Meth. Engng., 95(8): 685–720, 2013. DOI: 10.1002/nme.4538.
[verdugo_2014a] F. Verdugo, N. Parés, and P. Díez. Goal-oriented space-time adaptivity for transient dynamics using a modal description of the adjoint solution. Comput. Mech., 54(2): 331–352, 2014. DOI: 10.1007/s00466-014-0988-2.
[verdugo_2014b] F. Verdugo, N. Parés, and P. Díez. Error Assessment in Structural Transient Dynamics. Archives of Computational Methods in Engineering, 21(1): 59–90, 2014. DOI: 10.1007/s11831-014-9096-x.
[verdugo_2016a] F. Verdugo and W.A. Wall. Unified computational framework for the efficient solution of n-field coupled problems with monolithic schemes. Computer Methods in Applied Mechanics and Engineering, 310: 335–366, 2016. DOI: 10.1016/j.cma.2016.07.016.
[verdugo_2016b] F. Verdugo, C.J. Roth, L. Yoshihara, and W.A. Wall. Efficient solvers for coupled models in respiratory mechanics. International Journal for Numerical Methods in Biomedical Engineering, 2016. DOI: 10.1002/cnm.2795.
[verdugo_2019] F. Verdugo, A.F. Martín, and S. Badia. Distributed-memory parallelization of the aggregated unfitted finite element method. Computer Methods in Applied Mechanics and Engineering, 357, 2019. DOI: 10.1016/j.cma.2019.112583.